Funded by the National Science Foundation (NSF), USA: 09/2017 - 08/2020
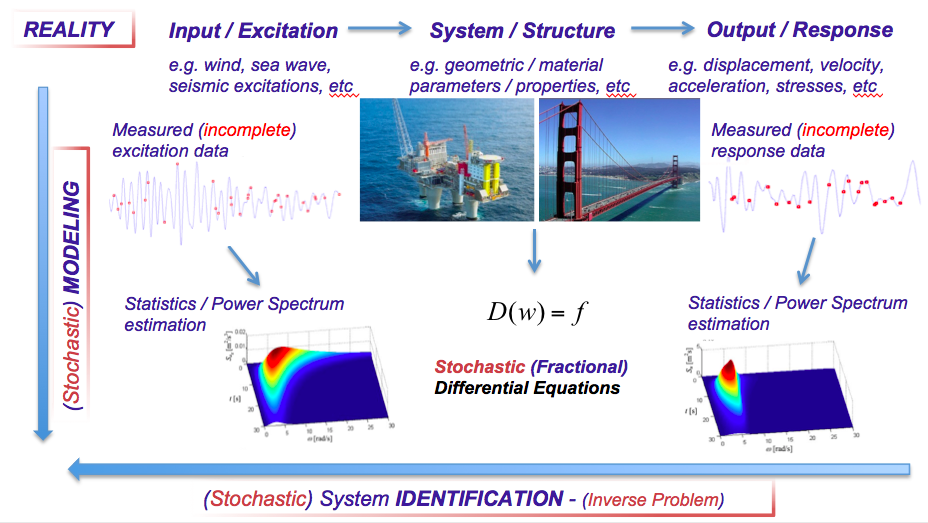
To efficiently analyze, design, optimize, and maintain structural and mechanical systems, uncertainties related to governing equations need to be handled rigorously and be properly accounted for. For instance, to restore and improve urban infrastructure, uncertainties related to ageing mechanisms and environmental excitations need to be identified and quantified. This relates to the development of methodologies for acquiring, interpreting, and translating raw data into pertinent stochastic models. Further, dynamical systems subject to environmental actions most often exhibit a time-varying and nonlinear behavior. In this regard, robust identification approaches are needed for formulating and solving an inverse problem to determine the structural system properties. The importance of such approaches is paramount for further development of system damage/fault detection procedures. Such diagnostic methods can be integrated in a broader framework for real-time monitoring of the dynamic behavior of the system as well as assessing its reliability. This project will focus on advancing knowledge in the fields of uncertainty modeling and quantification, with emphasis on stochastic excitation modeling and structural system identification subject to highly limited data. The project will have a broad academic impact and will contribute to diverse research fields such as structural dynamics, probabilistic methods, data acquisition and signal processing, as well as structural safety and reliability. In addition to the core research, the proposed innovative education and outreach plan will engage the general public in understanding the importance of uncertainties in engineering analysis and design, and will impact the advancement of next-generation researchers and practicing engineers. Students and educators will also benefit via the proposed teaching and learning innovations, and a special effort will be made to attract students from minorities and underrepresented groups in STEM education. Specifically, e-learning interactive software tools to be deployed online offering wide accessibility will be developed incorporating research results from this project into course material; while selected K-12 students and teacher-scholars will be mentored, trained, and assisted with their education and career goals.
Specific challenges related to modeling of the uncertainties, and the identification of the structural system properties based on knowledge of input-output (excitation-response) data include: (1): measured/available data most often possess evolutionary features, i.e. they exhibit a time-varying behavior, (2): most often there are limited, incomplete and/or missing data, and (3): the system governing equations are highly complex from a mathematics perspective, including nonlinearities and fractional derivatives modeling. Currently, it is not possible to address cases (1), (2), and (3) simultaneously in a consistent, efficient manner. The research objective of this project is to create a compressive sampling based methodology for efficient uncertainty modeling and quantification in the field of stochastic engineering dynamics subject to highly limited data. Specific goals include the development of techniques for spectral analysis and stochastic process statistics estimation subject to incomplete data, as well as for identifying the parameters of nonlinear systems endowed with fractional derivative elements. Preliminary work suggests satisfactory accuracy for up to 80% missing data.