Funded by the National Science Foundation (NSF), USA: 09/2018 - 08/2024
This CAREER award will support research that will contribute new knowledge in the field of stochastic engineering dynamics, promoting both the progress of science and advancing national prosperity. To analyze and eventually design structural systems, ranging from nano-resonators to civil infrastructure, requires potent mathematical tools to account for complex response behaviors as well as for the presence of uncertainties in the modeling process. Nevertheless, current state-of-the-art analysis techniques exhibit either the feature of high accuracy, or the feature of computational efficiency, but not both. This is inadequate for proper system analysis, design and optimization. This award supports fundamental research to adapt, extend, and apply path integral based mathematical tools to determine the response and assess the reliability of complex stochastic dynamical systems. The proposed methodology will have a major impact on the analysis and design of diverse dynamical systems and structures, and will contribute to a number of emerging technologies such as in nano-mechanics and energy harvesting. Therefore, results from this research will benefit the U.S. economy and society. Specifically, its unique feature of exhibiting both considerable accuracy and computational efficiency will push the current capabilities of stochastic analysis to unprecedented levels. This will lead to a paradigm shift in the optimization and design of diverse engineering systems ranging from nano-mechanical oscillators, to vibratory energy harvesters and civil infrastructure systems; thus, eventually reducing the cost and increasing the quality of such systems and structures. The diverse education and outreach plan will also impact the advancement of next-generation researchers and practicing engineers, as well as students and educators via the proposed teaching and learning innovations.
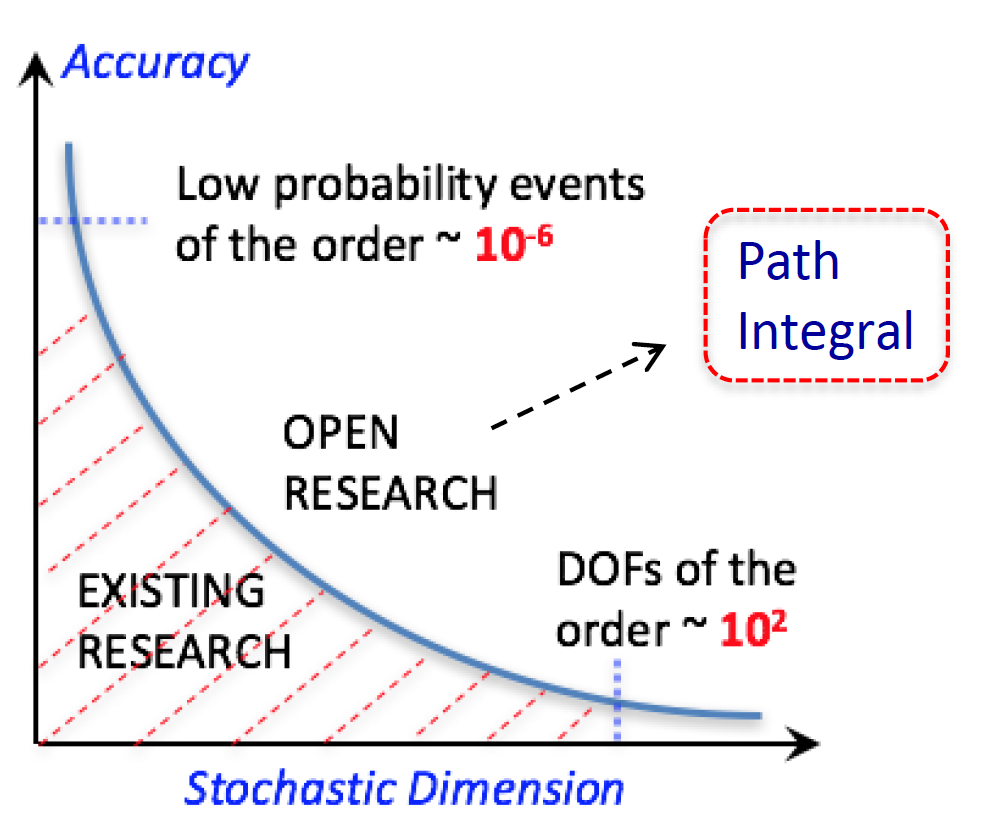
Available techniques for solving the governing equations and determining the stochastic response of dynamical systems can be broadly divided into two categories: a) those that exhibit high accuracy, but can handle a very small number of stochastic dimensions due to prohibitive computational cost, and b) those that can readily treat high-dimensional systems, but provide reliable estimates for low-order response statistics only (e.g. mean and standard deviation). In comparison to the current state-of-the-art techniques, the proposed path integral methodology will exhibit superior accuracy and computational efficiency. To achieve high accuracy the research approach is to account for higher order terms (fluctuations) in related path integral expansions. At the same time the error of the methodology will be quantified. To achieve high computational efficiency and account for a large number of stochastic dimensions (>100), the research approach is to explore highly sparse representations for the system response in conjunction with appropriate optimization algorithms. The methodology will also be versatile, accounting for cases of complex stochastic excitation and system modeling including fractional derivatives, and non-Gaussian, nonlinear, and hysteretic response behaviors.